第 7 章: 搜索
¶ 本章不会介绍任何新的 JavaScript 特定概念。相反,我们将一起解决两个问题,并在此过程中讨论一些有趣的算法和技术。如果你对这并不感兴趣,可以跳过本章。
¶ 让我介绍一下我们的第一个问题。请看这张地图。它显示了位于太平洋上的一个小热带岛屿——希瓦奥阿。
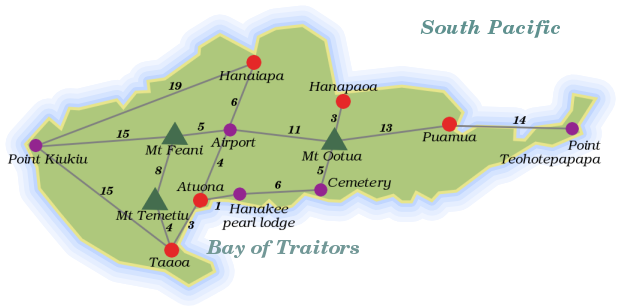
¶ 灰色线条是道路,旁边标注的数字是道路的长度。假设我们需要一个程序来查找希瓦奥阿上两点之间的最短路线。我们该如何着手呢?请思考一下。
¶ 真的,不要只是跳到下一段。试着认真思考一些解决方案,并考虑你可能遇到的问题。在阅读技术书籍时,很容易只是快速浏览文本,严肃地点头,然后立即忘记你读过什么。如果你认真努力解决一个问题,它就变成了你的问题,它的解决方案将更有意义。
¶ 这个问题的第一个方面是,再次,表示我们的数据。图片中的信息对我们的计算机来说意义不大。我们可以尝试编写一个程序来查看地图并提取其中的信息……但这可能会变得很复杂。如果我们有 20,000 张地图需要解释,这将是一个好主意,在这种情况下,我们将自己进行解释,并将地图转录成更适合计算机的格式。
¶ 我们的程序需要知道什么?它必须能够查找哪些位置是相连的,以及它们之间的道路有多长。岛上的地方和道路形成了一个 图,正如数学家所称呼的那样。存储图有很多方法。一个简单的可能性是只存储一个道路对象数组,每个对象都包含属性,命名它的两个端点及其长度……
var roads = [{point1: "Point Kiukiu", point2: "Hanaiapa", length: 19}, {point1: "Point Kiukiu", point2: "Mt Feani", length: 15} /* and so on */];
¶ 然而,事实证明,该程序在计算路线时,经常需要获取所有从特定位置开始的道路列表,就像站在十字路口的人会查看路标,并阅读 "Hanaiapa:19km,Mount Feani:15km"。如果这很容易(并且快速)做到,那就太好了。
¶ 对于上面给出的表示,我们必须每次都筛选整个道路列表,找出相关道路,就像我们想要查看路标列表一样。一个更好的方法是直接存储此列表。例如,使用一个对象,将地名与路标列表关联起来。
var roads = {"Point Kiukiu": [{to: "Hanaiapa", distance: 19}, {to: "Mt Feani", distance: 15}, {to: "Taaoa", distance: 15}], "Taaoa": [/* et cetera */]};
¶ 当我们拥有这个对象时,获取从 Point Kiukiu 出发的道路只需查看 roads["Point Kiukiu"] 即可。
¶ 然而,这种新表示包含重复信息:A 和 B 之间的道路在 A 和 B 下都列出来了。第一个表示已经非常繁琐了,这个更糟。
¶ 幸运的是,我们拥有计算机擅长重复工作的优势。我们可以指定道路一次,让计算机生成正确的数据结构。首先,初始化一个名为 roads 的空对象,并编写一个函数 makeRoad
var roads = {}; function makeRoad(from, to, length) { function addRoad(from, to) { if (!(from in roads)) roads[from] = []; roads[from].push({to: to, distance: length}); } addRoad(from, to); addRoad(to, from); }
¶ 不错吧?注意内层函数 addRoad 如何使用与外层函数相同的名称 (from、to) 作为其参数。这些不会冲突:在 addRoad 内部,它们指的是 addRoad 的参数,在外部,它们指的是 makeRoad 的参数。
¶ addRoad 中的 if 语句确保与 from 命名的位置相关联的目的地数组存在,如果没有,则它会放入一个空数组。这样,下一行就可以假设存在这样一个数组,并安全地将新道路推入其中。
¶ 现在地图信息看起来像这样
makeRoad("Point Kiukiu", "Hanaiapa", 19); makeRoad("Point Kiukiu", "Mt Feani", 15); makeRoad("Point Kiukiu", "Taaoa", 15); // ...
¶ 在上面的描述中,字符串 "Point Kiukiu" 仍然连续出现了三次。我们可以通过允许在一行中指定多条道路来使我们的描述更加简洁。
¶ 编写一个函数 makeRoads,它接受任意数量的奇数个参数。第一个参数始终是道路的起点,之后每对参数都给出终点和距离。
¶ 不要复制 makeRoad 的功能,而是让 makeRoads 调用 makeRoad 来进行实际的道路创建。
function makeRoads(start) { for (var i = 1; i < arguments.length; i += 2) makeRoad(start, arguments[i], arguments[i + 1]); }
¶ 此函数使用一个命名参数 start,并从 arguments(准)数组中获取其他参数。i 从 1 开始,因为它必须跳过第一个参数。i += 2 是 i = i + 2 的简写,你可能还记得。
var roads = {}; makeRoads("Point Kiukiu", "Hanaiapa", 19, "Mt Feani", 15, "Taaoa", 15); makeRoads("Airport", "Hanaiapa", 6, "Mt Feani", 5, "Atuona", 4, "Mt Ootua", 11); makeRoads("Mt Temetiu", "Mt Feani", 8, "Taaoa", 4); makeRoads("Atuona", "Taaoa", 3, "Hanakee pearl lodge", 1); makeRoads("Cemetery", "Hanakee pearl lodge", 6, "Mt Ootua", 5); makeRoads("Hanapaoa", "Mt Ootua", 3); makeRoads("Puamua", "Mt Ootua", 13, "Point Teohotepapapa", 14); show(roads["Airport"]);
¶ 我们通过定义一些方便的操作,成功地大大缩短了对道路信息的描述。可以说,我们通过扩展词汇,更简洁地表达了信息。 定义像这样的 "小语言" 通常是一种非常强大的技术——当你发现自己一直在编写重复或冗余的代码时,请停下来尝试创建一个词汇,使代码更短更密集。
¶ 冗余代码不仅令人厌烦,而且容易出错,人们在做不需要思考的事情时会不那么专注。最重要的是,重复代码很难更改,因为当结构被重复一百次,而它又恰好是错误或不理想时,就必须更改一百次。
¶ 如果你运行了上面所有的代码片段,现在你应该有一个名为 roads 的变量,其中包含岛上的所有道路。当我们需要从某个地方开始的道路时,我们可以直接做 roads[place]。但是,当有人在地名中拼写错误时(这在这些地名中并不罕见),他将得到 undefined 而不是他期望的数组,从而导致奇怪的错误。相反,我们将使用一个函数来检索道路数组,并在给出未知地名时向我们发出警告。
function roadsFrom(place) { var found = roads[place]; if (found == undefined) throw new Error("No place named '" + place + "' found."); else return found; } show(roadsFrom("Puamua"));
¶ 这是一个路径查找算法的第一个尝试,赌徒的方法。
function gamblerPath(from, to) { function randomInteger(below) { return Math.floor(Math.random() * below); } function randomDirection(from) { var options = roadsFrom(from); return options[randomInteger(options.length)].to; } var path = []; while (true) { path.push(from); if (from == to) break; from = randomDirection(from); } return path; } show(gamblerPath("Hanaiapa", "Mt Feani"));
¶ 在道路的每个分叉处,赌徒都会掷骰子,决定他应该走哪条路。如果骰子让他回到原来的路,那就这样吧。迟早,他将到达目的地,因为岛上的所有地方都由道路连接。
¶ 最令人困惑的一行可能是包含 Math.random 的那行。此函数返回 0 到 1 之间的伪随机 1 数字。尝试从控制台调用它几次,它将(很可能)每次都给你一个不同的数字。函数 randomInteger 将此数字乘以给定的参数,并使用 Math.floor 向下舍入结果。因此,例如,randomInteger(3) 将产生数字 0、1 或 2。
¶ 对于那些厌恶结构和计划,拼命寻找冒险的人来说,赌徒的方法是最好的选择。但我们着手编写一个程序,它可以找到两个地方之间的最短路线,因此需要其他方法。
¶ 解决此类问题的一种非常直接的方法被称为 "生成和测试"。它是这样的。
- 生成所有可能的路线。
- 在此集合中,找到实际上将起点连接到终点且最短的那条路线。
¶ 步骤二并不难。步骤一有点问题。如果你允许路线中包含循环,那么路线的数量将是无限的。当然,包含循环的路线不太可能是到任何地方的最短路线,而且不从起点开始的路线也不必考虑。对于像希瓦奥阿这样的小图,应该可以生成从某个点开始的所有非循环(无环)路线。
¶ 但首先,我们需要一些新工具。第一个是名为 member 的函数,它用于确定数组中是否找到某个元素。该路线将作为一个地名数组保存,当到达一个新地方时,该算法会调用 member 来检查我们是否已经到过该地方。它可能看起来像这样。
function member(array, value) { var found = false; forEach(array, function(element) { if (element === value) found = true; }); return found; } print(member([6, 7, "Bordeaux"], 7));
¶ 然而,这将遍历整个数组,即使该值立即在第一个位置找到。太浪费了。在使用 for 循环时,可以使用 break 语句跳出循环,但在 forEach 结构中,这将不起作用,因为循环体是一个函数,而 break 语句不会跳出函数。一种解决方案可能是调整 forEach 以识别某种类型的异常,以指示中断。
var Break = {toString: function() {return "Break";}}; function forEach(array, action) { try { for (var i = 0; i < array.length; i++) action(array[i]); } catch (exception) { if (exception != Break) throw exception; } }
¶ 现在,如果 action 函数抛出 Break,forEach 将吸收异常并停止循环。存储在变量 Break 中的对象仅用作比较对象。我给它一个 toString 属性的唯一原因是,这对于弄清楚你正在处理什么样的奇怪值可能会有用,如果你不知何故在 forEach 之外遇到了 Break 异常。
¶ 能够从 forEach 循环中跳出非常有用,但在 member 函数中,结果仍然相当难看,因为需要专门存储结果并在稍后返回它。我们可以添加另一种类型的异常,Return,它可以带有一个 value 属性,并且让 forEach 在抛出此异常时返回此值,但这将非常临时和混乱。我们真正需要的是一个全新的高阶函数,称为 any(有时也称为 some)。它看起来像这样
function any(test, array) { for (var i = 0; i < array.length; i++) { var found = test(array[i]); if (found) return found; } return false; } function member(array, value) { return any(partial(op["==="], value), array); } print(member(["Fear", "Loathing"], "Denial"));
¶ any 遍历数组中的元素,从左到右,并将测试函数应用于它们。第一次返回真值时,它将返回该值。如果未找到真值,则返回 false。调用 any(test, array) 或多或少等同于执行 test(array[0]) || test(array[1]) || ... 等等。
¶ 就像 && 是 || 的伙伴一样,any 也有一个名为 every 的伙伴
function every(test, array) { for (var i = 0; i < array.length; i++) { var found = test(array[i]); if (!found) return found; } return true; } show(every(partial(op["!="], 0), [1, 2, -1]));
¶ 另一个需要的函数是 flatten。此函数接收一个数组的数组,并将数组中的元素放在一个大的数组中。
function flatten(arrays) { var result = []; forEach(arrays, function (array) { forEach(array, function (element){result.push(element);}); }); return result; }
¶ 可以使用 concat 方法和某种 reduce 来完成相同的事情,但这效率较低。就像反复连接字符串比将它们放入数组然后调用 join 速度慢一样,反复连接数组会产生许多不必要的中间数组值。
¶ 在开始生成路线之前,还需要一个高阶函数。这个函数叫做 filter。像 map 一样,它接收一个函数和一个数组作为参数,并产生一个新的数组,但它不是将调用函数的结果放入新数组中,而是产生一个数组,其中只包含旧数组中返回真值的那些值。编写此函数。
function filter(test, array) { var result = []; forEach(array, function (element) { if (test(element)) result.push(element); }); return result; } show(filter(partial(op[">"], 5), [0, 4, 8, 12]));
¶ (如果 filter 的应用结果令你感到意外,请记住,传递给 partial 的参数用作函数的第一个参数,因此它最终位于 > 的左侧。)
¶ 想象一下生成路线的算法是什么样的——它从起点开始,并开始为从那里出发的每条道路生成路线。在每条道路的尽头,它将继续生成更多路线。它不会沿着一条道路行驶,而是分支出去。因此,递归是模拟它的自然方式。
function possibleRoutes(from, to) { function findRoutes(route) { function notVisited(road) { return !member(route.places, road.to); } function continueRoute(road) { return findRoutes({places: route.places.concat([road.to]), length: route.length + road.distance}); } var end = route.places[route.places.length - 1]; if (end == to) return [route]; else return flatten(map(continueRoute, filter(notVisited, roadsFrom(end)))); } return findRoutes({places: [from], length: 0}); } show(possibleRoutes("Point Teohotepapapa", "Point Kiukiu").length); show(possibleRoutes("Hanapaoa", "Mt Ootua"));
¶ 该函数返回一个路线对象数组,每个对象包含路线经过的场所数组和长度。findRoutes 递归地继续一条路线,返回一个包含该路线的每个可能扩展的数组。当路线的终点是我们要去的地方时,它只是返回该路线,因为继续经过该地方将毫无意义。如果是另一个地方,我们必须继续。flatten/map/filter 行可能是最难理解的。这就是它所说的:'获取从当前位置出发的所有道路,丢弃那些前往这条路线已经经过的场所的道路。继续这些道路中的每一条,这将为每一条生成一个完成的路线数组,然后将所有这些路线放入一个我们要返回的大数组中。'
¶ 这一行做了很多事情。这就是良好的抽象有帮助的原因:它们允许你说出复杂的事情,而无需键入满屏的代码。
¶ 难道这不会永远递归下去,因为它不断地调用自身(通过 continueRoute)?不会,在某些时候,所有外出的道路都将通往路线已经经过的场所,filter 的结果将是一个空数组。对空数组进行映射将产生一个空数组,扁平化它仍然会得到一个空数组。因此,在死胡同上调用 findRoutes 会产生一个空数组,这意味着“没有办法继续这条路线”。
¶ 注意,场所是使用 concat 附加到路线中的,而不是使用 push。concat 方法创建一个新数组,而 push 修改现有的数组。由于该函数可能会从单个部分路线中分支出多条路线,因此我们不能修改表示原始路线的数组,因为它必须使用多次。
¶ 现在我们拥有所有可能的路线,让我们尝试找到最短的路线。编写一个函数 shortestRoute,它与 possibleRoutes 一样,接收起点和终点的名称作为参数。它返回一个单个路线对象,其类型与 possibleRoutes 生成的类型相同。
function shortestRoute(from, to) { var currentShortest = null; forEach(possibleRoutes(from, to), function(route) { if (!currentShortest || currentShortest.length > route.length) currentShortest = route; }); return currentShortest; }
¶ “最小化”或“最大化”算法中最棘手的事情是,在给出空数组时不要搞砸。在本例中,我们碰巧知道每两个地方之间至少有一条路,因此我们可以忽略它。但这有点糟糕。如果从 Puamua 到 Mount Ootua 的道路(陡峭而泥泞)被暴雨冲毁了怎么办?如果这导致我们的函数也崩溃,那将是一件很可惜的事情,因此它会注意在未找到路线时返回 null。
¶ 然后,非常函数式,抽象所有可以抽象的东西的方法
function minimise(func, array) { var minScore = null; var found = null; forEach(array, function(element) { var score = func(element); if (minScore == null || score < minScore) { minScore = score; found = element; } }); return found; } function getProperty(propName) { return function(object) { return object[propName]; }; } function shortestRoute(from, to) { return minimise(getProperty("length"), possibleRoutes(from, to)); }
¶ 不幸的是,它比另一个版本长三倍。在需要最小化多个事物的程序中,最好以这种方式编写通用算法,以便可以重复使用它。在大多数情况下,第一个版本可能就足够了。
¶ 注意 getProperty 函数,它在使用对象进行函数式编程时经常很有用。
¶ 让我们看看我们的算法在 Point Kiukiu 和 Point Teohotepapapa 之间找到了什么路线……
show(shortestRoute("Point Kiukiu", "Point Teohotepapapa").places);
¶ 在像 Hiva Oa 这样的小岛上,生成所有可能的路线并不需要太多工作。如果你尝试在比利时合理详细的地图上生成所有可能的路线,那将花费荒谬的时间,更不用说荒谬的内存了。尽管如此,你可能已经看到过那些在线路线规划器。这些规划器只需几秒钟就能为你提供通过庞大道路迷宫的或多或少最佳路线。他们是怎么做到的呢?
¶ 如果你留心,你可能已经注意到,没有必要生成所有一直到终点的路线。如果我们在构建路线时就开始比较路线,我们可以避免构建这个庞大的路线集,并且一旦找到一条到目的地的路线,我们就可以停止扩展已经比这条路线更长的路线。
¶ 为了尝试一下,我们将使用一个 20x20 的网格作为我们的地图

¶ 你在这里看到的是山区地形的高程图。黄色斑点是山峰,蓝色斑点是山谷。该区域被划分为边长为一百米的正方形。我们拥有一个名为 heightAt 的函数,它可以告诉我们该地图上任何正方形的高度(以米为单位),其中正方形由具有 x 和 y 属性的对象表示。
print(heightAt({x: 0, y: 0})); print(heightAt({x: 11, y: 18}));
¶ 我们想步行穿越这片地形,从左上角到右下角。网格可以被视为一个图。每个正方形都是一个节点,它与周围的正方形相连。
¶ 我们不喜欢浪费能量,所以我们更愿意走最轻松的路线。上坡比下坡更累,下坡比水平行走更累2。此函数计算两个相邻正方形之间的“加权米数”,这表示你从它们之间行走(或攀爬)时的疲惫程度。上坡的重量是下坡的两倍。
function weightedDistance(pointA, pointB) { var heightDifference = heightAt(pointB) - heightAt(pointA); var climbFactor = (heightDifference < 0 ? 1 : 2); var flatDistance = (pointA.x == pointB.x || pointA.y == pointB.y ? 100 : 141); return flatDistance + climbFactor * Math.abs(heightDifference); }
¶ 注意 flatDistance 计算。如果两个点在同一行或同一列上,则它们彼此相邻,它们之间的距离为一百米。否则,假设它们是对角线相邻的,两个这样的正方形之间的对角线距离为一百乘以二的平方根,约为 141。不允许对距离超过一步的正方形调用此函数。(它可以对此进行双重检查……但它太懒了。)
¶ 地图上的点由包含 x 和 y 属性的对象表示。这三个函数在处理此类对象时很有用
function point(x, y) { return {x: x, y: y}; } function addPoints(a, b) { return point(a.x + b.x, a.y + b.y); } function samePoint(a, b) { return a.x == b.x && a.y == b.y; } show(samePoint(addPoints(point(10, 10), point(4, -2)), point(14, 8)));
¶ 如果我们要在这张地图上找到路线,我们还需要一个函数来创建“路标”,即可以从给定点出发的方向列表。编写一个函数 possibleDirections,它接收一个点对象作为参数并返回一个附近点的数组。我们只能移动到相邻的点,包括直线和对角线,因此正方形最多有八个邻居。注意不要返回地图外的正方形。据我们所知,地图的边缘可能是世界的边缘。
function possibleDirections(from) { var mapSize = 20; function insideMap(point) { return point.x >= 0 && point.x < mapSize && point.y >= 0 && point.y < mapSize; } var directions = [point(-1, 0), point(1, 0), point(0, -1), point(0, 1), point(-1, -1), point(-1, 1), point(1, 1), point(1, -1)]; return filter(insideMap, map(partial(addPoints, from), directions)); } show(possibleDirections(point(0, 0)));
¶ 我创建了一个变量 mapSize,唯一目的是避免两次编写 20。如果在其他时间,我们想将此函数用于另一张地图,如果代码中充满了 20,而所有这些都需要更改,那就太笨拙了。我们甚至可以将 mapSize 设为 possibleDirections 的参数,以便我们可以将函数用于不同的地图,而无需更改它。但我认为在这种情况下没有必要这样做,因为这些事情可以在需要时随时更改。
¶ 那么为什么我没有添加一个变量来保存 0 呢,它也出现过两次?我假设地图总是从 0 开始,因此这种情况不太可能改变,为它使用一个变量只会增加噪音。
¶ 为了在不使浏览器因为计算时间过长而停止的情况下在地图上找到路线,我们必须停止业余的尝试,并实施一个严肃的算法。过去,人们对类似的问题投入了大量精力,并设计了许多解决方案(有些很出色,有些毫无用处)。一个非常流行且高效的算法被称为 A*(读作A-star)。本章的剩余部分将用于实现一个用于我们地图的A*寻路函数。
¶ 在进入算法本身之前,让我告诉你更多关于它解决的问题。通过图搜索路线的麻烦在于,在大型图中,路线的数量非常多。我们的Hiva Oa路径查找器表明,当图很小时,我们只需要确保路径不重复访问已经经过的点。在我们新的地图上,这已经不够了。
¶ 根本问题在于,有太多可能走错方向的空间。除非我们以某种方式引导路径探索朝着目标方向进行,否则我们为继续特定路径所做的选择更有可能走向错误的方向,而不是正确的方向。如果你继续这样生成路径,你最终会得到大量的路径,即使其中一条路径偶然到达了终点,你也无法知道它是否是最短路径。
¶ 所以,你想做的是探索更有可能首先到达终点的方向。在像我们地图这样的网格上,你可以通过检查路径的长度以及其终点与终点的距离来粗略估计路径的质量。通过将路径长度和其剩余距离的估计值相加,你可以大致了解哪些路径是很有希望的。如果你首先扩展有希望的路径,你就不太可能在无用的路径上浪费时间。
¶ 但这仍然不够。如果我们的地图是完全平坦的平面,看起来最有希望的路径几乎总是最好的路径,我们可以使用上述方法直接走到目标。但我们有山谷和山坡阻挡我们的路径,因此很难提前判断哪个方向是最有效的路径。由于这一点,我们最终仍然不得不探索太多路径。
¶ 为了纠正这一点,我们可以巧妙地利用我们始终首先探索最有希望路径这一事实。一旦我们确定路径A是到达点X的最佳方式,我们就可以记住这一点。当稍后路径B也到达点X时,我们知道它不是最佳路线,因此我们不必进一步探索它。这可以防止我们的程序构建许多无用的路径。
¶ 因此,该算法的工作原理大致如下...
¶ 需要跟踪两部分数据。第一个称为开放列表,它包含仍需探索的部分路线。每条路线都有一个分数,该分数通过将其长度与其到目标的估计距离相加计算得出。该估计值必须始终是乐观的,它不应该高估距离。第二个是我们已经见过的节点集,以及带我们到达那里的最短部分路线。我们将这个称为到达列表。我们从向开放列表添加仅包含起始节点的路线开始,并在到达列表中记录它。
¶ 然后,只要开放列表中存在节点,我们就取出分数最低(最佳)的节点,并找到可以继续它的方式(通过调用possibleDirections)。对于它返回的每个节点,我们通过将它附加到原始路线来创建一条新路线,并使用weightedDistance调整路线的长度。然后在到达列表中查找每个新路线的终点。
¶ 如果该节点尚未在到达列表中,这意味着我们之前从未见过它,我们将新路线添加到开放列表中并在到达列表中记录它。如果我们曾经见过它,我们将比较新路线的分数与到达列表中路线的分数。如果新路线更短,我们用新路线替换现有路线。否则,我们丢弃新路线,因为我们已经看到了到达该点的更好方式。
¶ 我们继续这样做,直到我们从开放列表中获取的路线到达目标节点,在这种情况下我们找到了路线,或者直到开放列表为空,在这种情况下我们发现不存在路线。在我们的例子中,地图不包含无法逾越的障碍,因此始终存在路线。
¶ 我们如何知道我们从开放列表中获得的第一条完整路线也是最短的路线?这是因为我们只在路线具有最低分数时才会查看它。路线的分数是其实际长度加上剩余长度的乐观估计。这意味着,如果一条路线在开放列表中具有最低分数,那么它始终是到达其当前终点的最佳路线 - 另一条路线不可能后来找到到达该点的更好方式,因为如果更好,它的分数就会更低。
¶ 当为什么它能工作的细微之处仍然让你困惑时,不要感到沮丧。在思考像这样的算法时,之前见过“类似的东西”会帮助很多,它会给你一个参照点来比较方法。初学者不得不没有这样的参照点,这使得他们很容易迷失。只要意识到,这是高级的东西,全局阅读本章的其余部分,并在以后当你感觉想挑战时再回来。
¶ 我担心,对于算法的一个方面,我将不得不再次调用魔法。开放列表需要能够保存大量路线,并能够快速找到其中分数最低的路线。将它们存储在普通数组中,并在每次搜索时遍历整个数组,速度太慢了,所以我给你一种数据结构,称为二叉堆。你用new创建它们,就像Date对象一样,将用于“评分”其元素的函数作为参数传递给它们。生成的物体具有push和pop方法,就像数组一样,但pop始终返回分数最低的元素,而不是最后push的元素。
function identity(x) { return x; } var heap = new BinaryHeap(identity); forEach([2, 4, 5, 1, 6, 3], function(number) { heap.push(number); }); while (heap.size() > 0) show(heap.pop());
¶ 为了尽可能地提高效率,我们还需要做一些调整。Hiva Oa算法使用位置数组来存储路线,并在扩展路线时使用concat方法复制它们。这次,我们不能再复制数组了,因为我们将探索大量的路线。相反,我们使用一个“链”来存储路线。链中的每个对象都有一些属性,比如地图上的点,以及到目前为止路线的长度,它还有一个指向链中先前对象的属性。有点像这样
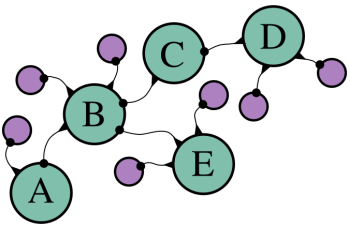
¶ 其中青色圆圈是相关的对象,线条代表属性 - 结尾带点的线条指向属性的值。对象A是此处路线的起点。对象B用于构建一条新的路线,该路线从A继续。它有一个属性(我们将其称为from),指向它所基于的路线。当我们稍后需要重建路线时,我们可以按照这些属性找到路线经过的所有点。请注意,对象B是两条路线的一部分,一条以D结尾,另一条以E结尾。当有很多路线时,这可以为我们节省很多存储空间 - 每条新路线只需要一个新的对象,其余部分与以相同方式开始的其他路线共享。
¶ 编写一个函数estimatedDistance,它提供两个点之间距离的乐观估计。它不必查看高度数据,但可以假设地图是平坦的。请记住,我们只沿着直线和对角线移动,并将两个方格之间的对角线距离计为141。
function estimatedDistance(pointA, pointB) { var dx = Math.abs(pointA.x - pointB.x), dy = Math.abs(pointA.y - pointB.y); if (dx > dy) return (dx - dy) * 100 + dy * 141; else return (dy - dx) * 100 + dx * 141; }
¶ 奇怪的公式用于将路径分解为直线部分和对角线部分。如果你有一个这样的路径...
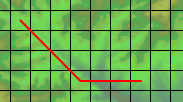
¶ ...路径宽度为6个方格,高度为3个方格,因此你得到6 - 3 = 3个直线移动和3个对角线移动。
¶ 如果你写一个函数,只计算点之间的直线“勾股”距离,那也行。我们需要一个乐观的估计,假设你可以直线走到目标当然是一种乐观的想法。但是,估计值越接近实际距离,程序需要尝试的无用路径就越少。
¶ 我们将使用二叉堆作为开放列表。到达列表的最佳数据结构是什么?它将用于查找路线,给定一对x,y坐标。最好是快速查找。编写三个函数,makeReachedList,storeReached和findReached。第一个创建你的数据结构,第二个给定一个到达列表,一个点和一条路线,将路线存储在其中,最后一个给定一个到达列表和一个点,检索路线或返回undefined表示没有为该点找到路线。
¶ 一个合理的想法是使用一个包含对象的物体。点中的一个坐标,例如x,用作外部对象的属性名称,另一个坐标y用作内部对象的属性名称。这确实需要一些簿记工作来处理这样一个事实,即有时我们正在寻找的内部对象不存在(尚未)。
function makeReachedList() { return {}; } function storeReached(list, point, route) { var inner = list[point.x]; if (inner == undefined) { inner = {}; list[point.x] = inner; } inner[point.y] = route; } function findReached(list, point) { var inner = list[point.x]; if (inner == undefined) return undefined; else return inner[point.y]; }
¶ 另一种可能性是将点的x和y合并成一个属性名称,并用它来在一个对象中存储路由。
function pointID(point) { return point.x + "-" + point.y; } function makeReachedList() { return {}; } function storeReached(list, point, route) { list[pointID(point)] = route; } function findReached(list, point) { return list[pointID(point)]; }
¶ 通过提供一组创建和操作这些结构的函数来定义数据结构类型是一种有用的技术。它可以将使用该结构的代码与结构本身的细节“隔离”。请注意,无论使用上述两种实现方法中的哪一种,需要到达列表的代码的工作方式完全相同。它不在乎使用什么类型的对象,只要它获得预期结果即可。
¶ 这将在第 8 章中详细讨论,在那里我们将学习如何创建像BinaryHeap这样的对象类型,这些类型使用new创建,并具有操作它们的方法。
¶ 这里我们终于有了实际的寻路函数
function findRoute(from, to) { var open = new BinaryHeap(routeScore); var reached = makeReachedList(); function routeScore(route) { if (route.score == undefined) route.score = estimatedDistance(route.point, to) + route.length; return route.score; } function addOpenRoute(route) { open.push(route); storeReached(reached, route.point, route); } addOpenRoute({point: from, length: 0}); while (open.size() > 0) { var route = open.pop(); if (samePoint(route.point, to)) return route; forEach(possibleDirections(route.point), function(direction) { var known = findReached(reached, direction); var newLength = route.length + weightedDistance(route.point, direction); if (!known || known.length > newLength){ if (known) open.remove(known); addOpenRoute({point: direction, from: route, length: newLength}); } }); } return null; }
¶ 首先,它创建了它需要的数据结构,一个开放列表和一个已到达列表。routeScore是赋予二叉堆的评分函数。注意它如何将结果存储在路由对象中,以避免多次重新计算它。
¶ addOpenRoute是一个便捷函数,它将一条新路线添加到开放列表和已到达列表中。它立即用于添加路线的起点。请注意,路线对象始终具有属性point,它保存路线末尾的点,以及length,它保存路线的当前长度。长度超过一个方格的路线还具有from属性,它指向它们的先前路线。
¶ while循环,如算法中所述,继续从开放列表中获取得分最低的路线,并检查这是否将我们带到目标点。如果不是,我们必须通过扩展它来继续。这就是forEach所要处理的。它在已到达列表中查找这个新点。如果在那里找不到它,或者找到的节点的长度大于新路线,则会创建一个新的路线对象并将其添加到开放列表和已到达列表中,并且现有路线(如果有)将从开放列表中删除。
¶ 如果known中的路线不在开放列表中怎么办?它必须在开放列表中,因为路线只有在被发现是到其终点的最优路线时才会从开放列表中删除。如果我们尝试从二叉堆中删除一个不在其上的值,它将抛出一个异常,所以如果我的推理是错误的,我们可能会在运行函数时看到一个异常。
¶ 当代码变得足够复杂,让你对它的一些东西产生怀疑时,添加一些检查以在出现问题时引发异常是一个好主意。这样,你就知道没有奇怪的事情“默默地”发生,当你破坏了一些东西时,你会立即看到你破坏了什么。
¶ 请注意,此算法不使用递归,但仍然设法探索所有这些分支。开放列表或多或少地接管了函数调用栈在 Hiva Oa 问题递归解中的作用——它跟踪仍然需要探索的路径。每个递归算法都可以通过使用数据结构来存储“仍然需要做的事情”来以非递归的方式重写。
¶ 好吧,让我们试试我们的寻路器
var route = findRoute(point(0, 0), point(19, 19));
¶ 如果你运行了上面所有的代码,并且没有引入任何错误,那么这个调用,尽管可能需要几秒钟才能运行,应该会给我们一个路线对象。这个对象很难阅读。这可以通过使用showRoute函数来解决,如果你的控制台足够大,它将在地图上显示一条路线。
showRoute(route);
¶ 你也可以将多条路线传递给showRoute,这在你想规划一条风景路线时可能很有用,比如这条路线必须包括11、17处的美丽观景点。
showRoute(findRoute(point(0, 0), point(11, 17)), findRoute(point(11, 17), point(19, 19)));
¶ 在图中搜索最佳路线的主题变体可以应用于许多问题,其中许多问题与找到物理路径毫无关系。例如,一个需要解决拼图的程序,将许多方块放入有限空间中,可以通过探索它通过尝试将某个方块放在某个位置而得到的各种“路径”来做到这一点。最终没有足够空间放置最后一个方块的路径是死胡同,成功放置所有方块的路径是解决方案。