附录 2: 二叉堆

¶ 在第七章中，二叉堆被介绍为一种以快速查找最小元素的方式存储对象集合的方法。如承诺的那样，本附录将解释这种数据结构背后的细节。

¶ 再次考虑我们需要解决的问题。A* 算法创建了大量的较小对象，并且必须将这些对象保存在一个“打开列表”中。它还不断地从这个列表中移除最小的元素。最简单的方法是将所有对象都保存在一个数组中，并在需要时搜索最小的对象。但是，除非我们有很多时间，否则这样做是不行的。在未排序的数组中查找最小元素需要遍历整个数组并检查每个元素。

¶ 当然，下一个解决方案是对数组进行排序。JavaScript 数组有一个很棒的sort 方法，可以用来完成繁重的工作。不幸的是，每次添加元素时都要重新排序整个数组，这比在未排序的数组中搜索最小值要花费更多的时间。可以使用一些技巧，例如，不是重新排序整个数组，而是确保新值插入到正确的位置，以便在排序之前已经排序的数组保持排序。这越来越接近二叉堆已经使用的方法，但在数组中间插入一个值需要将它后面的所有元素向上移动一个位置，这仍然太慢了。

¶ 另一种方法是不使用数组，而是将值存储在一个互连对象的集合中。一个简单的形式是让每个对象都保存一个值和两个（或更少）指向其他对象的链接。有一个根对象，保存最小的值，用于访问所有其他对象。链接始终指向保存较大值的 对象，因此整个结构看起来像这样

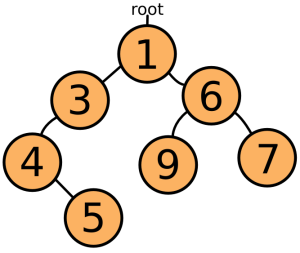
¶ 这种结构通常被称为树，因为它们的分支方式。现在，当你需要最小的元素时，你只需取走顶部的元素，然后重新排列树，使顶部元素的其中一个子元素——具有最低值的子元素——成为新的顶部。当插入新元素时，你“下降”树，直到找到一个小于新元素的元素，然后将其插入到那里。这比排序数组要少搜索很多，但它有一个缺点，就是会创建很多对象，这也降低了速度。

¶ 然后，二叉堆确实使用了排序数组，但它只是部分排序，就像上面的树一样。数组中的位置被用来形成一棵树，就像这张图片试图显示的那样

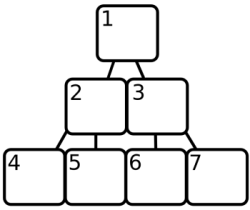
¶ 数组元素 1 是树的根，数组元素 2 和 3 是它的子元素，一般来说，数组元素 X 的子元素是 X * 2 和 X * 2 + 1。你可以明白为什么这种结构被称为“堆”。请注意，这个数组从 1 开始，而 JavaScript 数组从 0 开始。堆将始终保持最小的元素在位置 1，并确保对于数组中位置 X 的每个元素，位置 X / 2（向下取整）处的元素更小。

¶ 查找最小的元素现在只需要取位置 1 处的元素。但当这个元素被移除时，堆必须确保数组中没有留下任何空洞。为了做到这一点，它将数组中的最后一个元素移动到开头，然后将其与位置 2 和 3 的子元素进行比较。它很可能是更大的，所以它被交换成其中一个，并且这个与子元素进行比较的过程会针对新的位置重复，等等，直到它到达一个位置，在这个位置上它的子元素更大，或者到达一个位置，在这个位置上它没有子元素。

[2, 3, 5, 4, 8, 7, 6]
Take out 2, move 6 to the front.
[6, 3, 5, 4, 8, 7]
6 is greater than its first child 3, so swap them.
[3, 6, 5, 4, 8, 7]
Now 6 has children 4 and 8 (position 4 and 5). It is greater than
4, so we swap again.
[3, 4, 5, 6, 8, 7]
6 is in position 4, and has no more children. The heap is in order
again.

¶ 类似地，当必须将一个元素添加到堆中时，它被放在数组的末尾，并允许“向上冒泡”，通过反复将其与父元素交换，直到找到一个比新节点小的父元素。

[3, 4, 5, 6, 8, 7]
Element 2 gets added again, it starts at the back.
[3, 4, 5, 6, 8, 7, 2]
2 is in position 7, its parent is at 3, which is a 5. 5 is greater
than 2, so we swap.
[3, 4, 2, 6, 8, 7, 5]
The parent of position 3 is position 1. Again, we swap.
[2, 4, 3, 6, 8, 7, 5]
The element can not go further than position 1, so we are done.

¶ 请注意，添加或插入一个元素并不需要将其与数组中的每个元素进行比较。事实上，由于父元素和子元素之间的跳跃随着数组变大而变大，因此当我们有很多元素时，这种优势尤其明显1。

¶ 下面是二叉堆实现的完整代码。需要注意的是，不是直接比较放入堆中的元素，而是首先对它们应用一个函数（scoreFunction），这样就可以存储不能直接比较的对象。

¶ 此外，由于 JavaScript 数组从 0 开始，而父元素/子元素计算使用从 1 开始的系统，因此有一些奇怪的计算来进行补偿。

function BinaryHeap(scoreFunction){
  this.content = [];
  this.scoreFunction = scoreFunction;
}

BinaryHeap.prototype = {
  push: function(element) {
    // Add the new element to the end of the array.
    this.content.push(element);
    // Allow it to bubble up.
    this.bubbleUp(this.content.length - 1);
  },

  pop: function() {
    // Store the first element so we can return it later.
    var result = this.content[0];
    // Get the element at the end of the array.
    var end = this.content.pop();
    // If there are any elements left, put the end element at the
    // start, and let it sink down.
    if (this.content.length > 0) {
      this.content[0] = end;
      this.sinkDown(0);
    }
    return result;
  },

  remove: function(node) {
    var length = this.content.length;
    // To remove a value, we must search through the array to find
    // it.
    for (var i = 0; i < length; i++) {
      if (this.content[i] != node) continue;
      // When it is found, the process seen in 'pop' is repeated
      // to fill up the hole.
      var end = this.content.pop();
      // If the element we popped was the one we needed to remove,
      // we're done.
      if (i == length - 1) break;
      // Otherwise, we replace the removed element with the popped
      // one, and allow it to float up or sink down as appropriate.
      this.content[i] = end;
      this.bubbleUp(i);
      this.sinkDown(i);
      break;
    }
  },

  size: function() {
    return this.content.length;
  },

  bubbleUp: function(n) {
    // Fetch the element that has to be moved.
    var element = this.content[n], score = this.scoreFunction(element);
    // When at 0, an element can not go up any further.
    while (n > 0) {
      // Compute the parent element's index, and fetch it.
      var parentN = Math.floor((n + 1) / 2) - 1,
      parent = this.content[parentN];
      // If the parent has a lesser score, things are in order and we
      // are done.
      if (score >= this.scoreFunction(parent))
        break;

      // Otherwise, swap the parent with the current element and
      // continue.
      this.content[parentN] = element;
      this.content[n] = parent;
      n = parentN;
    }
  },

  sinkDown: function(n) {
    // Look up the target element and its score.
    var length = this.content.length,
    element = this.content[n],
    elemScore = this.scoreFunction(element);

    while(true) {
      // Compute the indices of the child elements.
      var child2N = (n + 1) * 2, child1N = child2N - 1;
      // This is used to store the new position of the element,
      // if any.
      var swap = null;
      // If the first child exists (is inside the array)...
      if (child1N < length) {
        // Look it up and compute its score.
        var child1 = this.content[child1N],
        child1Score = this.scoreFunction(child1);
        // If the score is less than our element's, we need to swap.
        if (child1Score < elemScore)
          swap = child1N;
      }
      // Do the same checks for the other child.
      if (child2N < length) {
        var child2 = this.content[child2N],
        child2Score = this.scoreFunction(child2);
        if (child2Score < (swap == null ? elemScore : child1Score))
          swap = child2N;
      }

      // No need to swap further, we are done.
      if (swap == null) break;

      // Otherwise, swap and continue.
      this.content[n] = this.content[swap];
      this.content[swap] = element;
      n = swap;
    }
  }
};

¶ 以及一个简单的测试...

var heap = new BinaryHeap(function(x){return x;});
forEach([10, 3, 4, 8, 2, 9, 7, 1, 2, 6, 5],
        method(heap, "push"));

heap.remove(2);
while (heap.size() > 0)
  print(heap.pop());